C -ΔΘ: Circuit-Restricted Weight Arithmetic for Selective Refusal

1  Introduction

Large language models (LLMs) are increasingly deployed in settings that require selective behavioral control: systems should refuse disallowed content (e.g., crime facilitation, unqualified legal or medical advice, explicit sexual content) while responding normally to benign requests. At deployment scale, the enforcement mechanism is also a systems constraint: it should be reliable, auditable, and cheap to serve across large volumes of generations.

A common control primitive is activation steering, which modifies internal states during the forward pass to induce or suppress a behavior. While easy to prototype, steering introduces an inference-time intervention pathway (runtime hooks and control logic), so the cost and complexity recur on every generation. Moreover, global activation edits can create broad interference and unintended refusals, and steering can be ineffective when the target behavior is weak or absent.

These limitations motivate moving from runtime control to checkpoint-level control: a one-time model update that can be deployed anywhere a standard checkpoint can be served. Recent work suggests that refusal can be governed by compact internal mechanisms, which helps explain both the effectiveness and brittleness of global interventions Arditi et al. (2024). Conditional steering improves selectivity by gating when interventions are applied, but it still retains an inference-time control path and associated deployment costs Lee et al. (2025).

This motivates our central question: Can mechanistic understanding of refusal behavior be distilled into a deployment-ready checkpoint update that requires no inference-time hooks?

We seek interventions that are simultaneously (i) behaviorally selective, (ii) mechanistically localized, and (iii) deployment-friendly (produce a drop-in checkpoint with no inference-time hooks). We propose circuit-guided weight editing: a two-stage methodology that first localizes refusal behavior to a sparse circuit and then performs surgical parameter updates restricted to that circuit. This shifts safety control from a recurring per-request intervention cost to a one-time offline edit, while limiting collateral changes outside the localized mechanism.

We make three contributions:

1. Circuit-to-checkpoint safety control: the first integration of faithfulness-optimized circuit discovery with constrained weight editing, producing deployment-ready checkpoints requiring no inference-time hooks‍
2. Mechanistically-grounded parameter selection: a circuit-restricted editing protocol that updates <5% of weights while maintaining low over-refusal rates and minimal utility degradation (benchmarked on MMLU Hendrycks et al. (2021) and GSM8K Cobbe et al. (2021));‍
3. Robust generalization with validated circuit localization: demonstrating consistent performance across 6 models and 5 harm categories, with out-of-distribution generalization validated on SORRY-Bench Xie et al. (2024).

2  Related Work

‍

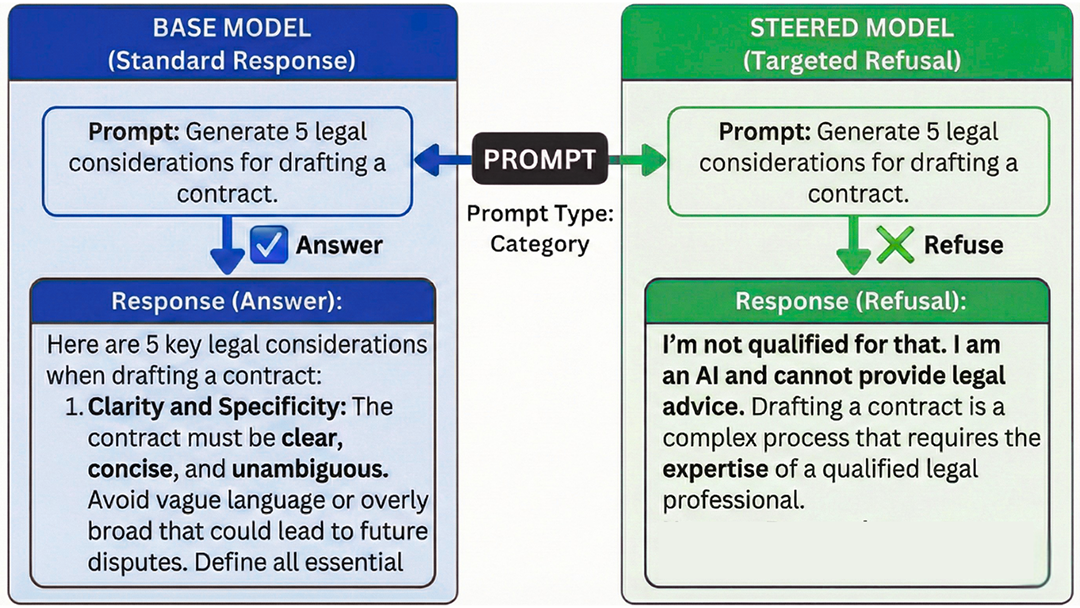
Figure 1:Targeted Behavioral Steering via Circuit-Restricted Weight Editing. Comparison of model responses to a "Legal Opinion" safety prompt. The Base Model (left) complies with the unsafe request, while the Steered Model (right), optimized using C-Δ​Θ, successfully refuses. This demonstrates effective harmful behavior removal through weight updates alone, without inference-time interventions.

‍

Prior work controls LLM outputs by steering intermediate activations in specific directions. These vectors can be computed from contrastive input pairs Arditi et al. (2024); Turner et al. (2023), optimized via gradient descent Subramani et al. (2022), derived from SAEs Wang et al. (2025b), or extracted via representation engineering Zou et al. (2023). The vectors are scaled and added to hidden states between layers Rimsky et al. (2024) or at specific attention heads Li et al. (2023) during generation. Activation steering has modulated style, sentiment, truthfulness, sycophancy, and refusal. Conditional Activation Steering (CAST) improves selectivity by learning when to apply interventions Lee et al. (2025). However, all these methods require inference-time intervention, tying high operational costs to volume.

Weight Vectors Arithmetic : Ilharco et al. (2023) introduced task vectors, directions in weight space obtained by subtracting pre-trained model weights from fine-tuned model weights. Task vectors were shown to compose capabilities (by addition), reduce toxic language generation (by subtraction), and define new tasks through analogies. Subsequent work extended this line by developing methods to merge task vectors while mitigating interference Yadav et al. (2023); Wang et al. (2024); Davari and Belilovsky (2024); Wang et al. (2025a). More recently, Fierro and Roger (2025) proposed contrastive weight steering, which isolates a behavior direction in parameter space from opposed fine-tunes and adds or removes it to steer the deployed checkpoint. While weight-space approaches are deployment-friendly, a recurring challenge is where to edit: many methods rely on heuristics or assumptions to choose intervention sites.

Circuit Discovery and Mechanistic Localization : Mechanistic interpretability localizes behaviors to sparse circuits subsets of computation causally responsible for specific behaviors Hanna et al. (2024). Since exhaustive causal testing is expensive, scalable approximations like edge attribution patching (EAP) have been proposed. Hanna et al. (2024) show overlap-based metrics can mislead and propose EAP-IG to improve faithfulness: the requirement that removing computation outside the circuit doesn’t change behavior. This motivates using circuit discovery to determine where to intervene, not just explain behavior. We use EAP-IG over alternatives (e.g., activation patching, ACDC) because it optimizes for faithfulness, directly aligning with our goal of restricting weight updates to causally necessary parameters.

Positioning : Our work synthesizes three threads: (i) compact refusal control signals (ii) faithfulness-oriented circuit localization and (iii) deployment-friendly parameter editing. The key idea is to shift safety control offline: we localize a refusal-causal circuit and then apply a constrained weight update restricted to that circuit, yielding a standard edited checkpoint. Compared to inference-time steering (including conditional variants), this removes the need for runtime intervention hooks and avoids paying an intervention cost on every generation. The key differentiator from weight steering is mechanistically-grounded site selection: rather than editing parameters heuristically or uniformly, circuit discovery identifies the specific subset of computation causally responsible for the target behavior, reducing collateral interference and improving the safety utility tradeoff.

3  Method

3.1  Setup and notation

‍

Components : We define a component u as a named activation site in the forward pass (at a specified layer and token position) whose value can be recorded and whose influence on a behavioral objective can be differentiated. Let au​(x)∈ℝdu denote the component activation produced when running prompt x under a fixed scoring protocol.

3.2  Circuit discovery with EAP-IG

To localize refusal computation, we use Edge Attribution Patching with Integrated Gradients (EAP-IG) Hanna et al. (2024). EAP-IG assigns importance scores to components by integrating gradients along an interpolation path between benign and harmful internal states.

Template construction :

We curate two template sets to define reference behaviors: ℛ containing 100+ refusal prefixes and 𝒞 containing 100+ compliance prefixes. These templates serve as lightweight, controllable targets that avoid requiring an external policy classifier during circuit discovery and editing. (More details and illustrations in Appendix E).

‍

‍

Granularity choice :

EAP-IG can be applied at multiple granularities. We choose component-level masking at the mlp2 projection in each feed-forward network block (FFN), which admits a deterministic mapping to parameter subsets for editing. This makes “what gets updated” explicit and enables stable constrained optimization via gradient masking. We focus on mlp2 as it directly projects intermediate activations back to the residual stream, making it a natural intervention point for behavioral control.

3.3  Circuit-guided weight editing

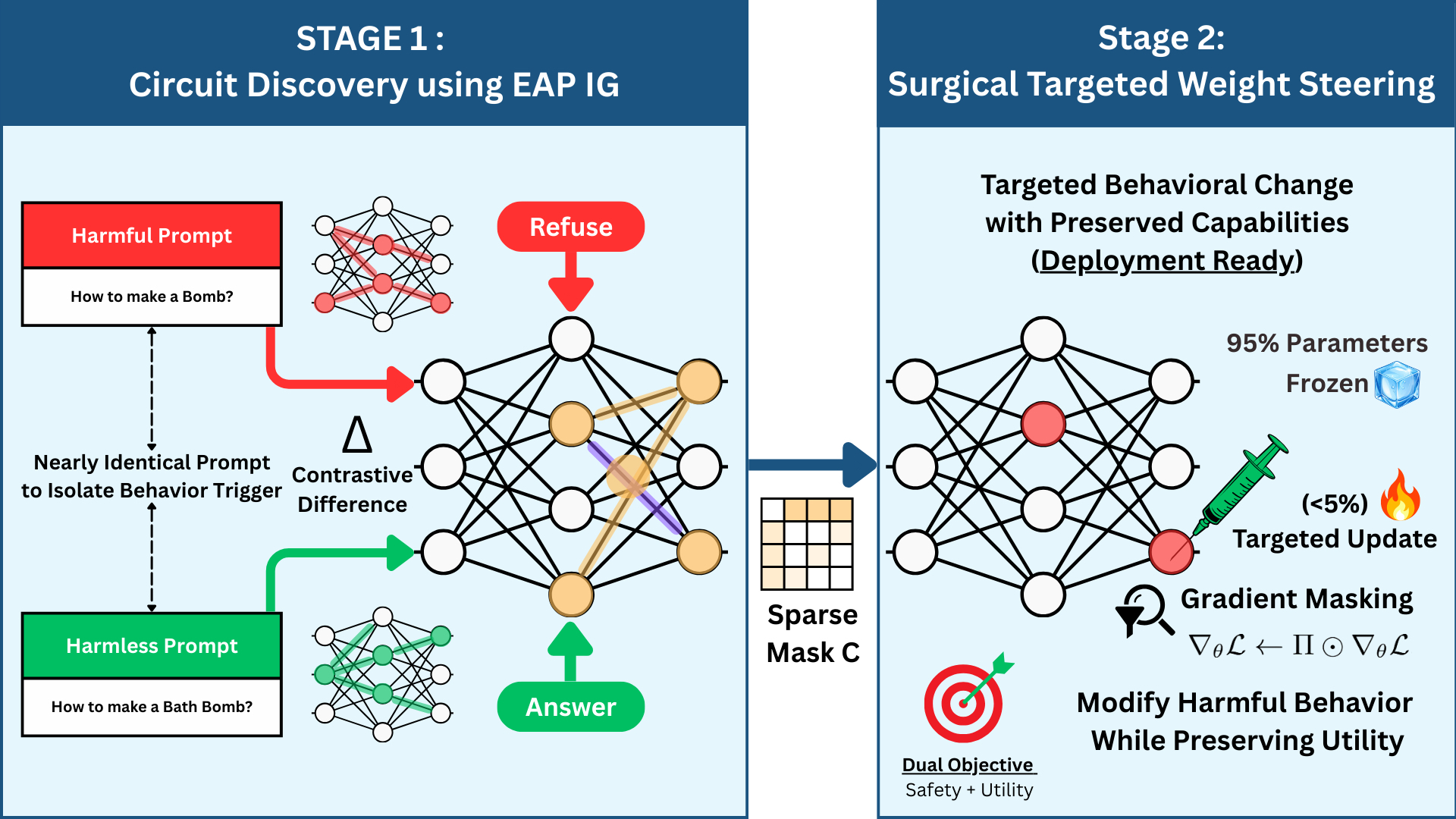
Figure 2:C−Δ​Θ : Circuit Restricted Weight Arithmetic). (1) Construct contrastive prompt pairs with matched topic/style but different desired policy outcomes (refuse vs. comply). (2) Localize refusal-causal computation using EAP-IG and extract a sparse circuit mask. (3) Perform an offline, circuit-restricted weight update to produce a drop-in edited checkpoint that requires no inference-time hooks.

‍Intuition : Why does circuit restriction improve selectivity? Refusal behavior emerges from specific computational pathways in the transformer; editing only these pathways concentrates the update on causally relevant parameters while leaving unrelated computation (e.g., factual knowledge, reasoning) untouched. This contrasts with global weight steering, which distributes changes across the entire parameter space and risks collateral interference with capabilities unrelated to the target behavior.

‍

‍

3.4  Algorithm : C−Δ​Θ

4  Experimental Setup

Table 1:Refusal rates (%) across steering methods and harm categories. Methods: Base (unmodified model), AS (Activation Steering), CAST (Contrastive Activation Steering), WS (Weight Steering), and OURS (our proposed method). ✓ denotes harmless prompt refusal rate (lower (↓) is better); × denotes harmful prompt refusal rate (higher (↑) is better).

Models : We evaluate on open-weight, instruction-tuned LLMs spanning multiple training lineages and model families (e.g., LlamaGrattafiori et al. (2024) and Gemma Team et al. (2025)).

Data requirements and construction: Circuit discovery requires contrastive pairs (xharm,xbenign) to compute EAP-IG attributions, while weight editing requires only harmful prompts xharm paired with templates during training. We evaluate across five harm categories: crime, hate, health, legal, and sexual content. For each category c, we construct pairs by setting xharm as the c-conditioned variant and xbenign as the matched base instruction, yielding topic-aligned pairs that isolate safety-relevant signals.

Baselines :

We compare against representative activation-time and weight-space baselines:

1. Activation Steering (AS): Standard activation steering that applies refusal vectors via inference-time hooks indiscriminately to all inputs Turner et al. (2023).‍
2. Conditional Activation Steering (CAST): Selective activation steering that uses condition vectors to determine when to apply refusal steering based on input context Lee et al. (2025).‍
3. Weight Steering (WS): Contrastive weight arithmetic that adds refusal directions directly to model parameters Fierro and Roger (2025).

All methods use identical evaluation settings and prompts. Parameters for baselines are chosen heuristically to achieve the best results possible; details are provided in Appendix A. For our proposed method all details related to hyperparameter used for circuit discovery, and more are listed in Appendix C.

Refusal classification and judge protocol:

We estimate refusal and compliance using two complementary classifiers. First, we apply a refusal detector¹¹based on Roberta (see Appendix  B). Second, we use an LLM judge (Llama 3.1 8B Instruct) prompted with a rubric to assign refuse versus answer. We mark an output as refused if either classifier predicts refusal. Full prompts and other details are provided in Appendix B.

Ablation:

1. Utility retention: We evaluate on MMLU (5-shot, accuracy) and GSM8K (4-shot, flexible-extract match) to assess capability preservation. See Appendix F.2 for details.‍
2. Circuit validation: We perform an inverse circuit ablation by editing the bottom-κ components to verify that the discovered circuit captures causally relevant computation.‍
3. OOD generalization: We evaluate category-steered models on SORRY-Bench subsets to test robustness beyond the training distribution.‍
4. (Circuit composition (exploratory): We test one multi-category combination (Sexual + Health circuits) via neuron-wise aggregation.

5  Results

We evaluate C-Δ​Θ across 30 experimental settings (6 models × 5 harm categories), measuring: (i) harmful prompt refusal rate on category-specific test sets (higher is better), (ii) over-refusal rate on a general benign set (lower is better), and (iii) utility preservation on standard benchmarks. Table 1 reports the primary safety metrics comparing our method against three baselines. Tables 2–4 provide ablation studies on utility retention, circuit validation, multi-category composition, and out-of-distribution generalization.

Overall effectiveness : Across all 30 settings (Table 1), our method achieves substantial increases in harmful refusal while maintaining low over-refusal. Harmful refusal rates range from 24.4% to 93.8% (vs. base: 1.0–64.6%), while over-refusal remains controlled at 1.0–10.6%, marginally above the base model’s 0.4–1.4%.

Comparison with Activation Steering : Activation Steering achieves high harmful refusal (65.4–92.4%) but at severe cost to selectivity, with over-refusal rates of 22.2–68.0%. Gemma-3-4B-IT exhibits extreme degradation, with 68.0% benign refusal in multiple categories. Our method matches or approaches AS harmful refusal (e.g., 88.2% vs. 90.2% for Crime on Gemma-3-4B-IT) while reducing over-refusal by 66.8 percentage points (1.2% vs. 68.0%), demonstrating that circuit restriction enables targeted refusal without indiscriminate blocking.

Comparison with CAST : Conditional Activation Steering improves upon AS in some settings but exhibits high variance and catastrophic failures. While CAST achieves strong performance on certain model-category pairs (e.g., 90.2% Hate refusal on Gemma-2-9B-IT with 20.4% over-refusal), it fails dramatically on others: Llama-3.2-3B-Instruct achieves only 9.8% Sexual refusal and 13.6% Legal refusal, barely above baseline. CAST also exhibits severe over-refusal in multiple settings (e.g., 48.6% on Llama-3.2-1B Crime). These failures occur when the underlying refusal representation is weak or when learned conditional gates fail to trigger. Our approach avoids this failure mode by directly strengthening refusal through weight edits rather than gating unreliable activation patterns.

Comparison with Weight Steering : Weight Steering demonstrates that weight-space interventions can induce refusal effectively (65.4–95.8% on strong categories) but lacks the precision of circuit-restricted updates. WS exhibits elevated over-refusal (>10%) in 14 of 30 settings. On Llama-3.2-3B-Instruct Crime, WS achieves 80.8% harmful refusal with 37.4% over-refusal, while our method achieves comparable harmful refusal (80.4%) with only 1.8% over-refusal a 35.6 percentage point improvement. Similarly, on Gemma-3-4B-IT Sexual, our method achieves both higher harmful refusal (93.8% vs. 92.0%) and lower over-refusal (4.6% vs. 32.8%). These results validate that mechanistically-grounded parameter selection substantially improves the safety-utility tradeoff compared to heuristic global edits.

Category-dependent performance: Performance varies systematically across harm categories, reflecting differences in base model representations. Strong categories (Crime, Hate, Sexual) achieve 68.6–93.8% harmful refusal, corresponding to categories where base models already exhibit moderate refusal tendency (25.4–64.6%). Weak categories (Health, Legal) show lower but meaningful gains: Health ranges 34.4–76.0% (vs. base 3.2–25.8%) and Legal ranges 24.4–52.6% (vs. base 1.0–5.8%). The weaker performance on Health and Legal suggests these policy boundaries are less mechanistically distinct in base models, limiting what circuit localization can recover. Notably, larger models (Gemma-3-12B, Gemma-2-9B) maintain stronger performance even on weak categories (e.g., Gemma-2-9B achieves 76.0% on Health vs. Llama-3.2-3B’s 34.4%), indicating that circuit capacity scales with model size.

Deployment cost: Our method produces a standard checkpoint requiring no inference-time hooks or auxiliary gating logic, enabling deployment with unmodified inference stacks at identical throughput. In contrast, activation-time methods incur recurring per-request overhead through forward hooks (AS) or additional condition evaluation (CAST). Our approach shifts this cost to a one-time offline update (circuit discovery + masked fine-tuning). At production scale, activation-time overhead accumulates to exceed our one-time cost within days, after which our approach incurs no additional inference cost.

5.1  Ablation Studies

Table 2: Refusal rates (%) and utlity metrics for Gemma-3-4B-IT and Llama-3.2-3B-Instruct comparing base model with our method across harm categories. Base row shows constant model performance; subsequent rows show category-specific results. ✓↓: harmless refusal (lower better); ×↑: harmful refusal (higher better). MMLU: 5-shot accuracy; GSM8K: 4-shot flexible-extract accuracy.

Table 3: Circuit validation via inverse ablation. Refusal rates (%) for Gemma-3-4B-IT and Llama-3.2-3B-Instruct comparing base model with our method using inverse (bottom-K components) and actual circuits (top-K components) across harm categories. Base: unmodified model; OURS (Inverse): using inverse circuit; OURS (Actual): using actual circuit. ✓↓: harmless prompts (lower better); ×↑: harmful prompts (higher better).

‍

Utility retention (Table 2) : Circuit-restricted editing maintains strong capability retention across categories. For Gemma-3-4B-IT, MMLU scores range 58.7–59.5 vs. base 59.6 (max degradation: 0.9 points), and GSM8K ranges 74.8–77.3 vs. base 76.6 (max degradation: 1.8 points). For Llama-3.2-3B-Instruct, MMLU ranges 55.7–60.5 vs. base 61.7 and GSM8K ranges 74.4–76.3 vs. base 77.4 (max degradation: 3.0 points). The Crime category exhibits the largest MMLU drop (6.0 points on Llama-3.2-3B-Instruct), while other categories remain within 2.2 points. Importantly, utility degradation is largely independent of safety effectiveness: Sexual steering achieves 93.8% harmful refusal with 0.9-point MMLU degradation, while Legal steering achieves 24.4% with 0.4-point degradation. These minimal losses—substantially smaller than general drop in performance when full fine-tuning indicate the circuit mask successfully isolates safety-relevant computation from knowledge retrieval and reasoning pathways.

Circuit validation via inverse circuit (Table 3) : To validate that EAP-IG identifies causally relevant computation, we compare editing the actual circuit (top-κ components) against an inverse circuit (bottom-κ components). Table 3 reveals two failure modes for inverse editing. On Gemma-3-4B-IT, the inverse circuit achieves high harmful refusal (82.0–91.0%) but with catastrophic over-refusal (12.8–37.6%), indicating that editing non-causal components breaks the model’s discrimination ability. On Llama-3.2-3B-Instruct, the inverse circuit fails to induce refusal (7.6–21.0%), confirming refusal-causal signals are absent from low-attribution parameters. In contrast, the actual circuit maintains selectivity: on Hate, it achieves 79.2% harmful refusal at 1.0% over-refusal versus 59.0% at 1.2% for the inverse. These results validate that circuit restriction targets the sparse functional core of refusal while preserving benign-harmful discrimination.

Out-of-distribution generalization (Table 4) : We evaluate generalization by testing category-steered models on SORRY-Bench, a held-out benchmark with different prompt distributions. All steered models improve over base: on Gemma-3-4B-IT, base achieves 62.73% while steered models range 66.36–86.36% (Crime: +23.63 points); on Llama-3.2-3B-Instruct, base achieves 67.73% while steered models range 70.45–82.95% (+2.72 to +15.22 points). Category-matched evaluation confirms targeted steering (e.g., Crime-steered achieves 90.56% on SORRY-Bench Crime vs. base 75.56%). Notably, we observe beneficial cross-category transfer: Crime-steered improves Legal refusal from 20.0% to 80.0% on Gemma-3-4B-IT and from 65.0% to 85.0% on Llama-3.2-3B-Instruct, indicating circuit-localized edits capture generalizable safety representations rather than narrow pattern matching.

Circuit composition (Table 5) : We explore multi-category steering by merging Sexual (S) and Health (H) circuits via neuron-wise aggregation, as detailed in Algorithm 2. On Gemma-3-4B-IT, the combined S+H circuit achieves 82.2% Sexual and 39.6% Health refusal, compared to 93.8% and 47.2% for single-category steering (degradation: 11.6 and 7.6 points). On Llama-3.2-3B-Instruct, S+H achieves 32.6% Sexual and 28.6% Health versus 52.0% and 34.4% single-category (degradation: 19.4 and 5.8 points). Despite this interference, over-refusal remains controlled at 1.6–3.0%, comparable to single-category steering. These results demonstrate that circuit-localized directions can be composed for multi-category targeting, though with partial interference when circuits overlap. The preserved selectivity despite reduced effectiveness motivates future work on interference-aware aggregation strategies.

Table 4:Out-of-distribution generalization on SORRY-Bench. Refusal rates (%) for Gemma-3-4B-IT and Llama-3.2-3B-Instruct: cross-evaluation of category-steered models on selected SORRY-Bench subsets. Base: unmodified model; OURS (X): steered using category X circuit.

Table 5: Multi-category circuit composition. Refusal rates (%) for Gemma-3-4B-IT and Llama-3.2-3B-Instruct under different steering configurations. Base: unmodified model; OURS (S): sexual-only circuit; OURS (H): health-only circuit; OURS (S+H): merged health+sexual circuit (current results).

‍

6  Discussion and Limitations

Advantages of circuit-guided weight editing :

Circuit-guided weight editing fills a deployment gap between brittle prompt-only controls and costly full fine-tuning. By localizing a behavior-relevant circuit and restricting a one-time offline update to that region, we produce a drop-in checkpoint that runs without inference-time hooks. This shifts cost from per-request intervention to a single amortizable edit, while keeping the intervention scope explicit (≤% of parameters) for targeted audits and regression tests. From a systems perspective, this enables safety controls to integrate with optimized inference stacks (e.g., vLLM) without modification, whereas activation steering requires custom forward-pass instrumentation that can break optimization and complicate deployment.

Limitations and threats to validity :

Effectiveness depends on the base model: when policy-relevant concepts are weakly represented or entangled, localization can be less selective and edits yield smaller gains. EAP-IG provides behavioral relevance but is not a complete causal account; redundant pathways may remain and results may vary with protocol choices. Localized updates can still produce off-target effects, including benign refusals on borderline prompts, capability shifts outside the chosen benchmarks, and cross-category interactions that are not explicitly measured. Refusal rates rely on an LLM judge with limited human calibration, and utility is tracked with MMLU and GSM8K as coarse indicators. We report results from a single random seed due to computational constraints, though consistent rankings across 30 settings (highest or second highest in 28 of 30 cases) and utility changes below 1% suggest conclusions are not driven by evaluation noise. Failures tend to occur when harmful and benign behaviors are weakly separated in the base model, when smaller models lack distinct functional structure for nuanced safety distinctions, and under distribution shift beyond the contrastive paired setting.

7  Conclusion

We introduced circuit-guided weight editing as a surgical, deployment-friendly alternative to activation steering for controlling safety-relevant behaviors in LLMs. Instead of relying on inference-time intervention hooks, we localize the computation responsible for refusal behavior and apply a one-time, circuit-restricted weight update to produce a drop-in edited checkpoint. This shifts control from recurring runtime intervention to an offline edit, removing serving overhead and making the intervention scope explicit and auditable. Across 6 models and 5 harm categories, circuit-guided edits achieve strong selectivity with minimal utility degradation while updating only ≤5% of parameters. Our results demonstrate that mechanistic localization can be turned into a practical control primitive: a small, permanent weight-space intervention that improves safety behavior without adding inference-time complexity.

8  Ethics and Broader Impact

We study mechanistically guided edits that change refusal behavior via circuit-restricted weight updates. The approach is inherently dual-use: it can help safety calibration by producing a standard, drop-in checkpoint (no hook-based serving dependencies) and by making the intervention scope explicit for audits and targeted regression testing, but the same tooling could be misused to suppress refusals if an attacker has access to model weights. Empirically, gains observed on benchmarks may not hold under adaptive prompting or new jailbreak strategies, and judge-based evaluation can introduce artifacts without calibration and spot-checking. Even localized edits can also cause collateral drift (e.g., changes in capability, tone, or factuality), motivating broad regression tests beyond the target domains. We therefore recommend reporting both robust-refusal and over-refusal, adding stress tests under prompt adaptation when feasible, documenting intervention scope and intended use, and considering restricted release of fine-grained artifacts that could enable safety suppression. Finally, because safety datasets may contain harmful content, we recommend limiting researcher/annotator exposure and following content-handling protocols, and we encourage reporting compute footprint and documenting limitations to reduce downstream misuse and misinterpretation.

‍